1 引言
動力系數(shù)是起重機(jī)械設(shè)計與分析的重要參數(shù)之一。目前,在這方面的研究成果,大多集中于橋式類型起重機(jī)。本文應(yīng)用有限元法,研究了塔式起重機(jī)(簡稱塔機(jī))的動力特性,并提出了塔機(jī)動力系數(shù)簡化計算公式。經(jīng)實(shí)例驗(yàn)證、理論計算與實(shí)測結(jié)果相符,因此,有一定的實(shí)際參考價值。
2 動力系數(shù)的計算
用有限元法,將塔機(jī)空間桁架簡化為平面混合框架計算模型。吊重從地面提升時的激振荷載視為斜坡升載后保持恒定值,其動力響應(yīng)為:
吊重上升制動、下降制動的激振荷載視為階梯函數(shù),其動力響應(yīng)為:
以TQ1-6塔機(jī)為例,建立計算模型(圖1),略去阻尼。通過計算,得出在不同工況下,塔機(jī)各階主振型、各階主振型的固有頻率ω;所取各節(jié)點(diǎn)的位移、內(nèi)力、應(yīng)力。
利用動應(yīng)力與靜應(yīng)力之比,可求出各節(jié)點(diǎn)的動力系數(shù)ψ,即:
部分計算結(jié)果(幅度R=0.85m、起重量Q=6t、臂架平行軌道)繪成曲線見圖2~圖4。
為了解吊重從地面提升及下降制動過程中,塔機(jī)的振動情況,可計算出各節(jié)點(diǎn)在振動中不同時刻的位移,如圖5所示。同樣,也可計算出各節(jié)點(diǎn)在振動中不同時刻的內(nèi)力,如圖6所示。
3 動力系數(shù)的分析
由計算結(jié)果可知:
3.1 塔機(jī)是一個低頻振動系統(tǒng),且變形較大,在振動過程中,不僅有與荷載同方向的垂直振動,還有與荷載垂直的水平振動。由于水平慣性力的影響,使塔根動力系數(shù)明顯增大。所以,整個塔機(jī)采用同一個動力系數(shù),不符合實(shí)際情況。
圖1 計算模型
圖20.6m/s,吊重從地面提升時ψ(ω)-Q曲線
圖3 吊重從地面提升時ψ-V曲線
1.塔根 2.塔腰 3.塔頂 4.塔尖 5.變幅鋼絲繩 6.吊臂 7.吊鉤;V——吊重提升或下降速度。
圖4 吊重下降制動時ψ-V曲線
圖5 吊重從地面提升時的位移曲線
1.吊臂端水平位移 2.吊鉤垂直位移 3.吊臂端垂直位移 4.塔腰水平位移
圖6 吊重從地面提升時的內(nèi)力曲線
1.塔根彎矩 2.塔腰彎矩 3.塔尖彎矩
4.吊臂壓力 5.吊鉤拉力
3.2 同一工況下,吊重從地面提升時,各節(jié)點(diǎn)的動力系數(shù)均隨吊重提升的瞬時速度增加,呈線性增大。而吊重下降制動時,僅塔根、塔腰的動力系數(shù),在一定速度范圍內(nèi)呈線性增大,高于該速度,則以曲線變化。塔尖、塔頂、吊臂、吊鉤的動力系數(shù)均與吊重下降速度呈非線性關(guān)系。
3.3 同一幅度時,各節(jié)點(diǎn)的動力系數(shù)均隨吊重的減小而增大。但在任何情況下,非額定起重量與該時的動力系數(shù)之積總小于額定起重量與其對應(yīng)的動力系數(shù)之積,即ψ*Q<ψ額*Q額。因此,應(yīng)以額定工況來確定動力系數(shù)值。
3.4 吊臂、吊鉤的動力系數(shù)很接近,可以取同一數(shù)值。
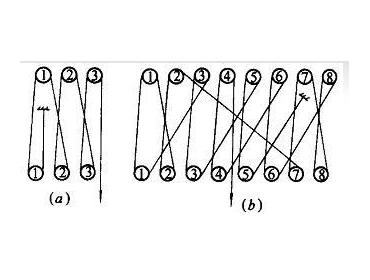
3.5 將吊重從地面提升與下降制動時相比較,見圖7。由此可知:在同一工況下,對于塔根、塔腰,當(dāng)?shù)踔貜牡孛嫣嵘龝r的動力系數(shù)較大;對于吊臂、吊鉤,當(dāng)?shù)踔卦谒C(jī)通常工作的速度范圍以內(nèi),下降制動時的動力系數(shù)較大。因此,確定動力系數(shù)時,塔身應(yīng)以吊重從地面提升時為準(zhǔn),而吊臂、吊鉤則以下降制動時為準(zhǔn)。
圖7 吊重從地面提升(虛線)與下降制動(實(shí)線)動力系數(shù)比較
1.塔根 2.塔腰 3.吊臂
4 動力系數(shù)的簡化計算
由圖5、圖6可知,塔機(jī)各點(diǎn)均近似地按第一振型作簡諧振動。所以可簡化為單質(zhì)點(diǎn)振動系統(tǒng)。
為此,首先將塔機(jī)簡化為圖8系統(tǒng)。吊臂轉(zhuǎn)化質(zhì)量、塔身轉(zhuǎn)化質(zhì)量、平衡臂轉(zhuǎn)化質(zhì)量與配重質(zhì)量之和分別為吊臂,塔身、平衡臂單位長度質(zhì)量與全長。
再根據(jù)能量等效原理簡化為圖9系統(tǒng),可得:
式中:x10——吊臂自由端ma處水平靜變位;
x20——塔頂mb處水平靜變位。
y10——吊臂自由端ma處垂直靜變位。
圖8
圖9
對于小車變幅塔機(jī),x10=x20=0.01h;y10=y(tǒng)c=0.02h。對于臂架變幅塔機(jī),x10=0.02h;y10=y(tǒng)20=0.01h。H為塔機(jī)高度。
最后,把m1、m2在m2處簡化為單質(zhì)點(diǎn)振動系統(tǒng),其垂直等效剛度為:
式中:Kyy——塔機(jī)在m1點(diǎn)的垂直剛度;
K2——鋼絲繩的剛度。
其等效質(zhì)量為:
式中:λ0——鋼絲繩的靜伸長〔一般取λ0=(0.02~0.03)h〕。
對于這樣的單質(zhì)點(diǎn)系統(tǒng),當(dāng)meq突然從地面提升時的動力系數(shù)為
式中:v0——吊重從地面提升時滑輪組的上升速度。
將Keq、meq代入上式得:
計算及實(shí)測表明,吊鉤與吊臂的動力系數(shù)很接近,且水平振動的慣性力對它們影響甚小,所以可按式(8)進(jìn)行計算。但對于吊鉤、吊臂,下降制動時的動力系數(shù)較大,所以引入下降制動影響系數(shù)β,其動力系數(shù)則為:
ψ=βψ1
式中:β——等于;Q——最大額定起重量。
由于塔身需要考慮水平振動的影響,所以引出水平動力系數(shù)ψx:
式中:FH——水平慣性力;
QF——Q的重力。
塔機(jī)在吊重從地面提升時所引起的振動是以基頻為主的低頻振動(可視為第一振型),所以:
在簡化計算中:m2與meq等速,y20=y(tǒng)eq,
將式(13)代入式(11)得:
水平動力系數(shù)為:
為求出塔身動力系數(shù),把水平動力系數(shù)折算為垂直動力系數(shù),由圖10可知,把水平慣性力FH折算為作用于吊臂端處y方向的力FV,兩者對塔根之矩相等,所以:
對塔根的折算動力系數(shù):
式中:x1d——臂端水平動位移;
y1d——臂端垂直動位移。
對于小車變幅塔機(jī),x1d=0.015h,y1d=0.03h。對于臂架變幅塔機(jī),x1d=0.03h,y1d=0.015h。因此,塔根的動力系數(shù)ψ2可用式表示:
ψ2=ψ1+〔(h-y1d+y10)/(R+x1d-x10)〕ψx(18)
同用樣方法可求出塔身任一點(diǎn)的動力系數(shù)。
圖10
因?yàn)閤10、y10、x1d、y1d與h相比很小,對于近似計算可以略去,即:
綜上所述,為簡便可將塔機(jī)各部位動力系數(shù)的計算公式統(tǒng)一表達(dá)為:
計算塔身時β=1,γ=1。計算吊鉤、吊臂時
以TQ1-6塔機(jī)為例,其主要部位的動力系數(shù)經(jīng)實(shí)測、理論計算、簡化計算,所得結(jié)果列于下表:
動力系數(shù)比較表
方法塔根吊鉤、吊臂
實(shí)測1.5401.133
理論計算1.5291.131
簡化計算1.6021.163
由此可見:理論計算、簡化計算與實(shí)測相符,本文提出的計算方法可靠。
 手機(jī)版|
手機(jī)版|

 關(guān)注公眾號|
關(guān)注公眾號|


 下載手機(jī)APP
下載手機(jī)APP